Circuitos Combinacionales: Fundamentos, Tipos y Aplicaciones

Los circuitos combinacionales son un pilar fundamental en la electrónica digital, utilizados en una amplia gama de aplicaciones, desde simples puertas lógicas hasta complejos sistemas de procesamiento. Se caracterizan por generar salidas que dependen exclusivamente del estado actual de las entradas, sin memoria de estados previos. Esta característica los distingue de los circuitos secuenciales, que dependen tanto de las entradas actuales como de los estados anteriores.

La importancia de los circuitos combinacionales radica en su capacidad para realizar operaciones lógicas y aritméticas esenciales en computadoras y otros dispositivos electrónicos. Estos circuitos se diseñan utilizando puertas lógicas básicas como AND, OR, y NOT, y se pueden representar y analizar mediante el uso del álgebra de Boole.

Diferencias entre Circuitos Combinacionales y Secuenciales

Para entender completamente los circuitos combinacionales, es crucial compararlos con los circuitos secuenciales. La diferencia principal entre ambos radica en cómo procesan y almacenan la información:

• Circuitos Combinacionales:
  • Las salidas dependen únicamente del estado actual de las entradas.
  • No poseen memoria interna; no recuerdan estados previos.
  • Se utilizan para operaciones lógicas y aritméticas inmediatas.
• Circuitos Secuenciales:
  • Las salidas dependen tanto del estado actual de las entradas como de los estados anteriores.
  • Tienen memoria interna, generalmente implementada con flip-flops.
  • Se utilizan para tareas que requieren almacenamiento temporal de información.

Tipos de Circuitos Combinacionales

Codificadores

Un codificador es un circuito que convierte información de un formato a otro. En su forma más simple, un codificador tiene 2^N entradas y N salidas, y su función es presentar en las salidas el código binario correspondiente a la entrada activada.

Tipos de Codificadores

• Codificadores sin Prioridad:
  • Solo una entrada puede estar activa a la vez.
  • Utilizados cuando no hay conflicto de señales múltiples.
  • Ejemplo: Un codificador de 4 a 2 líneas, donde solo una entrada está activa en un momento dado.
• Codificadores con Prioridad:
  • Pueden manejar múltiples entradas activas simultáneamente.
  • Codifican la señal de mayor prioridad.
  • Ejemplo: Un codificador de 4 a 2 líneas con prioridad, que codifica la entrada de mayor valor decimal cuando múltiples entradas están activas.

Decodificadores

Un decodificador realiza la operación inversa de un codificador, convirtiendo un código binario de N bits en 2^N salidas únicas. Es fundamental en aplicaciones como la selección de líneas en memoria y la activación de señales específicas.

• Ejemplo: Decodificador de 2 a 4 líneas:
  • Tiene 2 entradas y 4 salidas.
  • Cada combinación de las entradas activa una salida específica.

Multiplexores

Un multiplexor es un circuito que selecciona una de varias líneas de entrada y la transmite a una única línea de salida, controlado por señales de selección.

• Ejemplo: Multiplexor de 4 a 1:
  • Tiene 4 líneas de entrada, 2 líneas de selección y 1 salida.
  • Las líneas de selección determinan cuál de las entradas se conectará a la salida.

Demultiplexores

El demultiplexor es el dispositivo opuesto al multiplexor. Toma una sola línea de entrada y la dirige a una de varias líneas de salida basándose en las señales de selección.

• Ejemplo: Demultiplexor de 1 a 4:
  • Tiene 1 entrada, 2 líneas de selección y 4 salidas.
  • La señal de entrada se dirige a una de las salidas según las líneas de selección.

Comparadores

Los comparadores son circuitos que comparan dos valores binarios y determinan su relación de igualdad, mayor que o menor que.

• Ejemplo: Comparador de 4 bits:
  • Compara dos números de 4 bits y produce tres salidas indicando si el primer número es mayor, igual o menor que el segundo.

Sumadores

Los sumadores son circuitos que realizan operaciones de suma en binario. Existen dos tipos principales:

• Medio Sumador:
  • Tiene dos entradas y dos salidas: suma y acarreo.
  • Realiza la suma básica de dos bits.
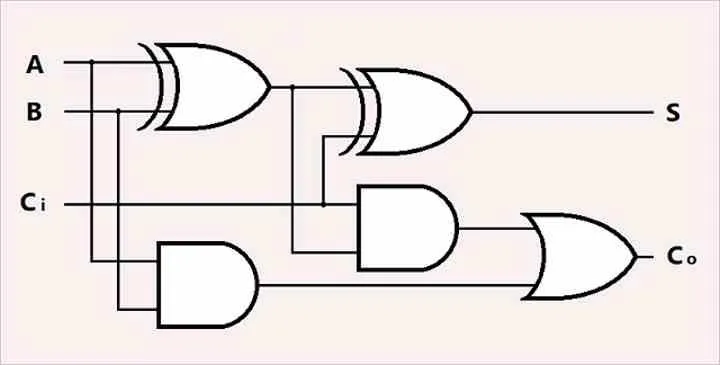
• Sumador Completo:
  • Tiene tres entradas: dos bits a sumar y un acarreo de la posición anterior.
  • Se construye usando dos medios sumadores.
  • Utilizado en la construcción de sumadores de varios bits.

Ejemplos Prácticos de Circuitos Combinacionales

Veamos algunos ejemplos detallados con diagramas y tablas de verdad para ilustrar el funcionamiento de los circuitos combinacionales.

Ejemplo 1: Codificador 4 a 2 sin Prioridad

Entrada	Salida
E3 E2 E1 E0	C1 C0
0 0 0 1	0 0
0 0 1 0	0 1
0 1 0 0	1 0
1 0 0 0	1 1

Ejemplo 2: Decodificador 2 a 4

Entrada	Salida
A1 A0	D3 D2 D1 D0
0 0	0 0 0 1
0 1	0 0 1 0
1 0	0 1 0 0
1 1	1 0 0 0

Ejemplo 3: Multiplexor 4 a 1

Selección	Salida
S1 S0	Y
0 0	I0
0 1	I1
1 0	I2
1 1	I3

Aplicaciones de los Circuitos Combinacionales

Los circuitos combinacionales se utilizan en diversas aplicaciones dentro de la electrónica digital y los sistemas de computadoras.

En Electrónica Digital

• Sistema de Control de Semáforos: Utiliza decodificadores para determinar cuál luz se enciende en base a un contador.
• Teclados de Computadora: Codificadores para convertir la pulsación de teclas en códigos binarios enviados a la computadora.

En Sistemas de Computadoras

• ALU (Unidad Aritmético-Lógica): Utiliza sumadores, restadores y comparadores para realizar operaciones aritméticas y lógicas.
• Gestión de Memoria: Multiplexores y demultiplexores para direccionar y seleccionar líneas de memoria.

En Telecomunicaciones

• Multiplexación de Señales: Multiplexores para combinar varias señales en un solo canal de comunicación.
• Desmultiplexación: Demultiplexores para separar señales combinadas en sus componentes individuales.

Álgebra de Boole Aplicada a los Circuitos Combinacionales

El álgebra de Boole es la base matemática para el diseño y análisis de circuitos combinacionales. Permite la simplificación de expresiones lógicas y la optimización de circuitos.

Conceptos Básicos de Álgebra de Boole

• Variables Booleanas: Pueden tomar valores de 0 o 1.
• Operaciones Booleanas: AND (·), OR (+), NOT (¬).
• Leyes de Boole: Incluyen leyes de identidad, complementación, idempotencia, absorción, distribución, entre otras.

Aplicación en el Diseño de Circuitos

• Simplificación de Expresiones: Utilizando las leyes de Boole para reducir el número de puertas lógicas necesarias.
• Diseño de Tablas de Verdad: Creación de tablas que muestren todas las combinaciones posibles de entradas y sus salidas correspondientes.
• Mapa de Karnaugh: Herramienta para simplificar funciones booleanas visualmente, reduciendo el número de términos.

Ejemplo de Simplificación

Para un circuito con la función lógica F(A,B,C)=A′B′C+AB′C+ABC′

Usando el teorema de consenso:

F = A′B′C+AB′C+ABC′

A′B′C+AB′C+ABC′ = B′C(A′+A)+ABC′

B′C(A′+A)+ABC′ = B′C+ABC′

Ventajas y Desventajas de los Circuitos Combinacionales

Ventajas

• Simplicidad: Más fáciles de diseñar y entender comparados con los circuitos secuenciales.
• Velocidad: No dependen de estados previos, lo que permite una respuesta rápida.
• Predecibilidad: Las salidas son directamente predecibles a partir de las entradas actuales.

Desventajas

• Falta de Memoria: No pueden almacenar información, lo que limita su uso en aplicaciones donde se requiere seguimiento de estados.
• Combinación de Entradas: En casos de muchas entradas, el número de combinaciones posibles aumenta exponencialmente, lo que puede complicar el diseño y análisis.

---

Esperamos que te haya gustado el articulo, te invitamos a leer